在行测的五大模块中，数量是令考生最头疼的一科。而在数量这一模块中，排列组合又考得尤其多(根据内蒙古考情)，也是比较难的一章。因此，今天就来给大家梳理一下排列组合问题中对应的一组题型以及其解题技巧。

一、“在一起”

在排列组合中，往往会遇到一类特殊的问题，比如，在做排列的时候两个或者多个要排列的元素需要放在一起，即他们之间不能分开。碰到这种问题的时候，就要将题目分成两步来做，首先，先将不能分开的部分进行排列(内部排列)，接着将已经排列好的部分看成一个整体，和其他部分一起排列(外部排列)，我们将这种方法叫做捆绑法，具体我们来看一道例题。

例：某美术馆计划展出12幅不同的画，其中有3幅油画、4幅国画、5幅水彩画，排成一行陈列，要求同一种类的画必须连在一起，并且油画不放在两端，问有多少种不同的陈列方式?

A.不到1万种 B.1万—2万种之间

C.2万—3万种之间 D.超过3万种

我们观察一下，这道题有明显的要求“必须连在一起”，这就提示我们要用捆绑法来解题了。因此，在做排列组合的问题时，如果看到了题干中有如下字眼：不能分开，连在一起，紧挨着等等，就可以判定本题用捆绑法求解了。

具体我们来看下解题思路：

第一步，本题考查排列组合问题，用捆绑法解题。

第二步，3幅油画捆绑在一起，4幅国画捆绑在一起，5幅水彩画捆绑在一起，一共3个整体，但是油画不能在两端，则油画必须在中间，那么国画和水彩画在两端有

=2(种)方式，3幅油画内部有

=6(种)方式，4幅国画内部有

=24(种)方式，5幅水彩画内部有

=120(种)方式，那么一共有2×6×24×120=34560>30000(种)。

因此，选择D选项。

简单总结一下，在用捆绑法解题时，记住一句话，先绑后排，即先做内部排列再做外部排列。

二、“不在一起”

与“在一起”题意恰恰相反，在做排列的时候两个或者多个要排列的元素一定不能放在一起，即他们之间一定要分开。碰到这种问题的时候，同样要将题目分成两步来做，首先，先将剩余的部分进行排列(剩余排列)，接着将不能放在一起的部分逐个插入到刚刚已经排列好的空隙里(插空)，这么说有点抽象，具体我们来看一道例题。

例：将三盆同样的红花和四盆同样的黄花摆放成一排，要求三盆红花互不相邻，共有多少种不同的方法?

A.10 B.8

C.15 D.20

我们观察一下，这道题有明显的要求“互不相邻”，这就提示我们要用插空法来解题了。因此，在做排列组合的问题时，如果看到了题干中有如下字眼：必须分开，互不相邻等等，就可以判定本题用插空法求解了。

具体我们来看下解题思路：

第一步，本题考查排列组合问题，用插空法解题。

第二步，根据红花互不相邻，四盆黄花有5个空，将三盆红花分别插到空中去，共有

=10(种)。

因此，选择A选项。

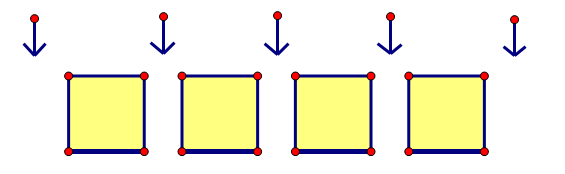
针对这个解析，可以看下图，黄色方块代表黄花，箭头指的部分就是空隙了。

总结一下，在用插空法解题时，记住一句话，先排后插，即先做剩余排列再进行插空。

针对排列组合解题技巧我们可以总结如下：